Poisson Distribution

The Poisson distribution models the number of events that occur in a fixed interval of time, space, or area, given that these events happen with a constant rate and independently of each other. The Poisson distribution can be used to model a phenomenon where we are waiting for an occurrence with respect time intervals i.e., count of events occurring in a fixed interval of time or space, given the average rate lambda λ.

Some examples would be waiting for a bus, waiting for customer arrivals in a store at a given hour, adverse events occurring during clinical trial, counting the number of mutations in a given stretch of DNA and in spatial distributions where we want to model the distribution of missile or drone hits in an area or even the distribution of fishes in a lake.

In Poisson distribution, the basic assumption is that for small time intervals, the probability of an arrival is proportional to the length of the waiting time. The Poisson distribution has a single parameter ƛ, also called the intensity parameter. In R, dpois(x, lambda) gives the PMF, and ppois(k, lambda) gives the CDF.

Probability Mass Function (PMF):

If X ∼ Poisson(λ), where:

• λ is the expected number of events (mean rate) in the given interval,
• X is the number of events in the interval,

The PMF is given as:

where:

• e ≈ 2.718 is the base of the natural logarithm,
• x! is the factorial of x.

Cumulative Distribution Function (CDF):

The CDF of the Poisson distribution, P(X ≤ k), is the sum of the probabilities for all integers up to k:

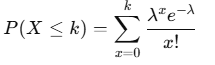
Mean:

E[X] = λ

Variance:

Var(X) = λ

Applications

• Healthcare: Modeling the number of patient arrivals in an emergency room per hour.
• Pharmaceuticals: Estimating the number of drug defects in a batch of medicines.
• Hospitals: Modeling the number of surgeries performed in a day.

Problem

Let’s look at a problem to better understand this distribution by going through it both manually & with R.

Manual Calculation of Poisson Probability

An Emergency Room in a hospital receives an average of 5 emergency cases per hour. Calculate:

1. The probability of receiving exactly 3 emergency cases in an hour.

P(X = 3) = (5³⋅e⁻⁵)/3! ​= (125 x 0.0067)/6 = 0.1404.

There is 14% chance of 3 patients arriving in to the ER.

2. What is the probability of receiving at most 2 cases.

‘At most’ means ‘less than or equal to’; in this case 2 or P(X ≤ 2). We apply CDF formula.

P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)

Using the PMF formula for each x:

P(X = 0) = (5⁰⋅e⁻⁵)/0! = e⁻⁵ = 0.0067,
P(X = 1) = (5¹⋅e⁻⁵​)/1! = 5 x 0.0067​ = 0.0337,
P(X = 2) = (5²⋅e⁻⁵)/2!​ = (25 x 0.0067​)/2 = 0.0839.
P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2) = 0.0067 + 0.0337 + 0.0839 = 0.1243

The chance of having at most 2 patients in an hour is 12%.

3. What is the probability of receiving at least 2 patients in an hour (CDF)?

P(X ≥ 2) = 1 − P(X < 2)
Since P(X < 2) = P(X ≤ 1) = P(X = 0) + P(X = 1) and from earlier results we sum it up.
P(X < 2) = P(X ≤ 1) = P(X = 0) + P(X = 1) = 0.0067 + 0.0337 = 0.0404
P(X ≥ 2) = 1 − P(X < 2) = 1 – 0.0404 = 0.9596

There is ~96% chance to receive at least 2 patients in an hour.

Calculating Poisson Probability Using R

# Parameters

> lambda <- 5 # Mean rate (average number of events)
> x <- 3 # Specific number of events

# 1. PMF for P(X = 3)

> P_X_equals_3 <- dpois(x, lambda = lambda)
> P_X_equals_3

# 2. CDF for P(X ≤ 2)

> P_X_less_equal_2 <- ppois(2, lambda = lambda)
> P_X_less_equal_2

# 3. CDF for P(X ≥ 2)

> P_X_greater_equal_2 <- 1 – ppois(1, lambda = lambda)
> P_X_greater_equal_2