Logistic Distribution

The logistic distribution is a continuous probability distribution used primarily in logistic regression and machine learning for modeling probabilities, as well as in growth models. It is similar in shape to the normal distribution but has heavier tails.

Probability Density Function (PDF)

The PDF of the logistic distribution is given by:

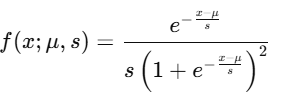
where:

• μ is the location parameter (median of the distribution),
• s>0 is the scale parameter (related to the spread),
• e is Euler’s number (≈2.718).

Cumulative Distribution Function (CDF)

The CDF of the logistic distribution is:

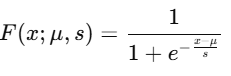
Mean & Variance

Mean = μ

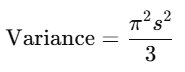
Applications of Logistic Distribution

1. Logistic Regression: Used to model probabilities in binary classification problems.
2. Growth Models: Used to describe growth curves (e.g., population growth).
3. Healthcare: Used in dose-response models in pharmacology.
4. Economics: Models price distributions and demand curves.
5. Machine Learning: Activation functions like the sigmoid in neural networks are derived from the logistic distribution’s CDF.

Problem Statement

Suppose the time to recovery for patients after a minor surgery follows a logistic distribution with:

• μ=10 hours (median recovery time),
• s=2 hours (scale parameter).

Find:

1. The probability that a patient recovers in less than 12 hours.
2. The probability that a patient takes more than 15 hours to recover.
3. The likelihood that a patient recovers exactly at 12 hours.

1. Probability of recovery in less than 12 hours (CDF):

P(X≤12) = F(12;μ,s) = 1/(1+e^{−(12−10)/2}) = 1/(1+e⁻¹) ≈ 1/(1+0.3679) = 1/1.3679 ≈ 0.7311.

So, there is a 73.11% chance of recovery in less than 12 hours.

2. Probability of taking more than 15 hours to recover (Complement of CDF):

P(X>15)=1−F(15;μ,s) = 1−[1/1+e^{−(15−10)/2}]=1−[1/(1+e^−2.5)]=1−[1/(1+0.0821)] = 1−(1/1.0821) ≈1−0.9231 = 0.0769.

So, there is a 7.69% chance of taking more than 15 hours to recover.

3. Likelihood of recovery exactly at 12 hours (PDF):

f(12;μ,s)=e^{−(12−10)/2}/2[(1+e^{−(12−10)/2})²] =e⁻¹/2(1+e⁻¹)² =0.3679/2⋅(1.3679)² ≈0.3679/2⋅1.8717 = 0.3679/3.7434 ≈ 0.0982.

The likelihood of recovery exactly at 12 hours is 0.0982. The probability, however, is 0 because the logistic distribution is continuous.

Working with R

# Parameters

> mu <- 10 # Location parameter (median)
> s <- 2 # Scale parameter

# 1. Probability of recovery in less than 12 hours (CDF)

> p_less_12 <- plogis(12, location = mu, scale = s)
> p_less_12

# 2. Probability of recovery taking more than 15 hours (Complement of CDF)

> p_more_15 <- 1 – plogis(15, location = mu, scale = s)
> p_more_15

# 3. Likelihood of recovery exactly at 12 hours (PDF)

> pdf_exact_12 <- dlogis(12, location = mu, scale = s)
> pdf_exact_12