Baye’s Theorem

Bayes’ Theorem is a fundamental concept in probability theory and statistics that describes the probability of an event, based on prior knowledge of conditions that might be related to the event. It provides a way to update our beliefs about the probability of an event based on new evidence or information. This theorem is closely related to the concept of conditional probability.

Bayes’ Theorem is stated mathematically as follows:

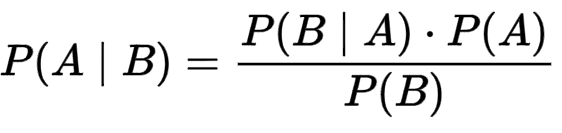
Where:

P(A): Prior probability (anterior) – the probability of event A before knowing B.
P(A∣B): Posterior probability – the updated probability of A after observing B.
P(B∣A): Likelihood – the probability of observing B given A is true.
P(B): Marginal likelihood – the total probability of B under all possible events.

Bayes’ theorem allows us to reverse conditional probabilities. Bayes’ theorem has extensive application in data mining such as text classification, spam filtering, and sentiment analysis.

Imagine a medical diagnostic test for a rare disease:

• Prior P(A): The probability of a patient having the disease (based on population data).
• Likelihood P(B∣A): The probability of getting a positive test result given the patient has the disease.
• Posterior P(A∣B): The probability of the patient having the disease given a positive test result.
• Marginal likelihood P(B): The total probability of a positive test (whether the patient has the disease or not).

The probability of having the disease P(A) is 0.05 (5%). The test correctly identifies the disease with 95% sensitivity (true positive rate) P(B∣A) = 0.95, but has a false positive rate of 10%, meaning that 10% of healthy patients test positive P(B∣A^c) = 0.10.
Given that a patient has tested positive, what is the probability that the patient actually has the disease?

We need to find P(A∣B), the probability of having the disease given a positive test result. Using Bayes’ Theorem:

P(A∣B) = (P(B∣A) × P(A)) / P(B)

where P(B), the probability of testing positive can be calculated using the Total Probability Rule:

P(B) = P(B∣A) × P(A) + P(B∣A^c) × P(A^c);
P(B) = (0.95×0.05) + (0.10×0.95) = 0.1425

Now, calculate P(A∣B):

P(A∣B) = (0.95×0.05) / 0.1425 = 0.333

Thus, given a positive test result, the probability that the patient actually has the disease is 0.333 (or 33.3%).