One-way ANOVA is a statistical test used to compare the means of three or more groups to see if there is a statistically significant difference among them. The null hypothesis assumes that all group means are equal, while the alternative hypothesis suggests that at least one group mean is different.
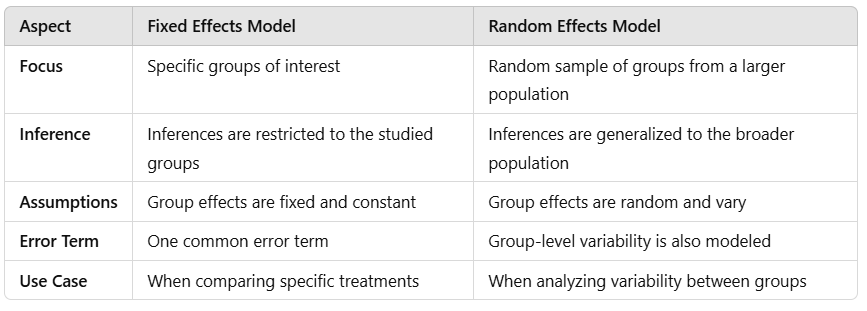
Fixed effects and random effects are two different types of models used to analyze data that have groupings or clusters.
1. Fixed Effects Model
In a fixed effects model, the levels of the factor (e.g., different groups) are considered fixed and are the primary focus of the study. The assumption is that you are analysing only those specific levels (groups) and aren’t interested in generalizing beyond them.
When to use: Use a fixed effects model when:
- You are working with specific groups, and these groups are the only ones of interest.
- You want to compare particular treatments, categories, or groups where the focus is on their unique impact on the outcome.
Interpretation: Each group (level) has its own mean, and you are testing the differences between these fixed group means.
2. Random Effects Model
In a random effects model, the levels of the factor are considered random samples from a larger population. This model assumes that the levels (groups) are not of primary interest, but rather you want to make inferences about the entire population from which the groups were drawn.
When to use: Use a random effects model when:
- You are dealing with groups that represent a random sample of a broader population, and you are interested in making generalizations beyond those specific groups.
- The groups are treated as random, and their effect is considered a source of random variability.
Interpretation: You are more concerned with the variability among groups rather than the specific differences between individual groups.
Example in R: Fixed Effects Model
Let us use the built-in ‘mtcars’ dataset to compare the mean miles per gallon (mpg) for cars with different numbers of cylinders (4, 6, 8). Here, we treat the number of cylinders as fixed effects.
# Load data
data(mtcars)
# One-way ANOVA with fixed effects
fixed_model <- aov(mpg ~ factor(cyl), data = mtcars)
# Summary of the model
summary(fixed_model)
Example in R: Random Effects Model
If you were to treat the number of cylinders as random effects, you would use the lme4 package, which allows for random effects modeling.
# Install and load the package
library(lme4) # Random
effects model (for demonstration)
random_model <- lmer(mpg ~ (1|factor(cyl)), data = mtcars) # Summary of the model summary(random_model)
Some examples where you use Fixed Effects vs Random Effects
You are only interested in these specific drugs and want to know which one performs better among these three. ( Use Fixed Effects).
A pharmaceutical company is studying the effectiveness of a new drug across different hospitals. Compare the effectiveness of the drug in three specific hospitals (Hospital A, Hospital B, Hospital C). (Use Fixed Effects).
A pharmaceutical company is studying the effectiveness of a new drug across different hospitals. Assess the variability in drug effectiveness across a random sample of hospitals. (Use Random Effects).
Using functions for both models
The aov() function in R, by default, assumes a fixed effects model. If random effects are to be modeled, they require the use of specialized packages such as lme4 (for linear mixed-effects models) or nlme. For random effects, lme4::lmer() or nlme::lme() is better suited.
Whatever we went so far with 1-way ANOVA is based on fixed effects model. This section was just to introduce to random effects model.
