F-test

An F-test is a type of statistical test that is used to compare two variances or to test the overall significance of a regression model. The F-test checks whether the variances of two populations are significantly different. It is commonly used in ANOVA (Analysis of Variance) and linear regression analysis.

The F-test is typically applied in the following scenarios:

1. Variance Comparison: Comparing the variances of two independent samples (to check if they come from populations with equal variances).
2. ANOVA: To compare means across multiple groups by analysing variance.
3. Regression Analysis: To assess whether at least one predictor variable in a multiple regression model significantly affects the response variable.

The F-statistic is calculated as the ratio of two variances:

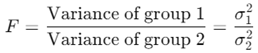
Where:

• σ₁²​ and σ₂²​ are the sample variances of the two groups.

The null hypothesis (H₀) states that the variances of the two groups are equal:

H₀: σ₁² = σ₂²​

The alternative hypothesis (H₁) can be either one-sided or two-sided, depending on the specific test:

H₁: σ₁²≠ σ₂²​ (for a two-tailed test)

Key Differences Between F-Test and T-Test

• F-Test compares variances while the t-test compares means.
• The F-test is used in ANOVA and regression, while the t-test is used to compare two means (either paired or independent).
• The F-distribution is positively skewed (right-skewed), and the values range from 0 to ∞. It is used to calculate the p-value in F-tests. In contrast, the t-distribution is symmetric around 0.

Let’s explore a scenario where two drug formulations are being tested to see if their effects (measured in terms of patients’ improvement scores) have significantly different variances. This test will determine if the variability in responses to the drugs is significantly different, which could inform researchers about the consistency or risk of the drug’s effects.

Problem

Imagine you’re a pharmaceutical researcher analysing the effectiveness of two new drug formulations (Drug A and Drug B) designed to lower blood pressure. Both drugs were given to two separate groups of patients, and the improvement in blood pressure was recorded for each patien

You want to test whether the variability (or variance) in blood pressure improvement between the two groups is significantly different. If the variances differ, it could indicate that one drug is more consistent in its effect than the other. This could be an important factor in deciding which drug formulation is more reliable for patients.

Group 1 (Drug A):  BP Improvement scores: 23, 26, 22, 24, 28, 27, 25
Group 2 (Drug B):  BP Improvement scores: 17, 19, 16, 18, 20, 21, 18S

Hypothesis:

We are interested in testing if the variances of the two groups are significantly different.

Null Hypothesis (H₀): The variances of both groups are equal. (No significant difference in variance).

H₀: σ₁² = σ₂²

Alternative Hypothesis (H₁): The variances of both groups are not equal. (There is a significant difference in variance).

H₁: σ₁² ≠ σ₂²

Performing test using R:

> drugA <- c(23, 26, 22, 24, 28, 27, 25)
> drugB <- c(17, 19, 16, 18, 20, 21, 18)
> var.test(group1, group2)

Interpretation & Results:

• F-statistic: 2.2449. This means the variance of Group 1 is 2.2449 times the variance of Group 2.
• p-value: 0.2476. Since this value is greater than the common significance level of 0.05, we fail to reject the null hypothesis. This means there is no significant difference in the variances of the two groups.

Thus, based on the test, we conclude that the variability in blood pressure improvements between Drug A and Drug B is statistically similar.

In drug testing, analyzing the variability in drug responses is crucial. Even if the mean effect of two drugs is similar, a drug with a higher variance may be less desirable because it may lead to unpredictable effects in different patients. On the other hand, a drug with low variance suggests more consistent effects across patients.

When performing statistical tests in pharmaceutical studies, both the mean (t-test) and variance (F-test) matter. A drug with high variability might cause issues in clinical practice, even if its mean effect looks good.