Continuous probability distributions describe the behavior of continuous random variables, which can take an infinite number of values within a range. These distributions are represented using probability density functions (PDFs) and are defined over intervals, not specific values. Some of the continuous distributions are normal, standard normal, uniform, exponential, gamma.
Key Characteristics
1. Continuous Random Variable (CRV)
A variable X is continuous if it can assume any value in a range, such as real numbers in [a,b], with infinite possible outcomes.
2. Probability Density Function (PDF)
- The PDF f(x) represents the relative likelihood that X takes on a value at xxx.
- Unlike discrete variables, the probability for a single point is zero:P(X=x)=0.
- The total area under the curve is 1.
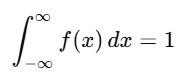
- The probability for an interval [a,b][a, b][a,b] is given by:
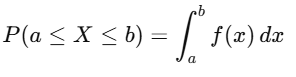
3. Cummulative Distribution Function (CDF):
- The CDF F(x) gives the probability that X is less than or equal to x:
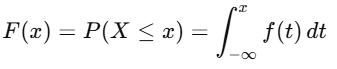
Properties:
- F(x) is a non-decreasing function.
- F(−∞)=0 and F(∞)=1.
- P(a≤X≤b)=F(b)−F(a).
4. Expected Value (Mean):
The mean μ=E[X] represents the average value of X:
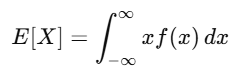
5. Variance and Standard Deviation:
Variance σ2 = Var(X) measures the spread of X:
Var(X)=E[X2]−(E[X])2
Standard deviation σ:
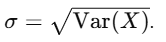
6. Moment Generating Function (MGF)
The MGF MX(t) is defined as:
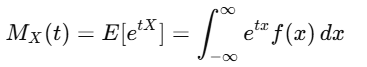
Moments (mean, variance, etc.) can be derived by differentiating MX(t).
