For heavily skewed sets of data an datasets that do not appear to me normally distributed, you should use Chebyshev rule instead of the empirical rule. The Chebyshev rule states that for any data set, regardless of the shape the percentage of values that are found within distances of k standard deviation from the mean must be at least (1 – 1/k2) * 100. For example, if the value of k is 2, then 1 – (1/22) *100 = 75% of the values are found within +/-2 standard deviations of the mean.
| Interval | Chebyshev any distribution | Empirical normal distribution |
| (μ-σ, μ+σ) | At least 0% | Approx. 68% |
| (μ-2σ,μ+2σ) | At least 75% | Approx. 95% |
| (μ-3σ,μ+3σ) | At least 88.89% | Approx. 99.7% |
A population of 2-liter bottles of cola is known to have a mean fill weight of 2.06 liter and a standard deviation of 0.02 liter. However, the shape of the population is unknown and you cannot assume that it is bell-shaped. Describe the distribution of fill-weights. Is it very likely that a bottle will contain less than 2 liters of cola?
(μ ± σ) = 2.06 ± 0.02 = (2.04, 2.08)
(μ ± 2σ) = 2.06 ± 2(0.02) = (2.02, 2.10)
(μ ± 3σ) = 2.06 ± 3(0.02) = (2.00, 2.12) Because the distribution may be skewed, we cannot use the empirical rule. Using the Chebyshev rule, you cannot say anything about the percentage of bottles containing between 2.04 & 2.08 liters. You can state that at least 75% of the bottles will contain between 2.02 & 2.10 liters and at least 88.89% will contain between 2.00 & 2.12 liters. Therefore, between 0 & 11.11% of the bottle will contain less than 2 liters.
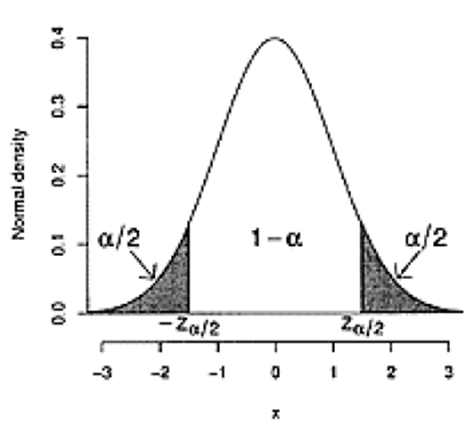
The below picture shows the relationship between Z, α, α/2. The shaded regions are called the critical region (left tail & right tail).