Parametric & Non-parametric data

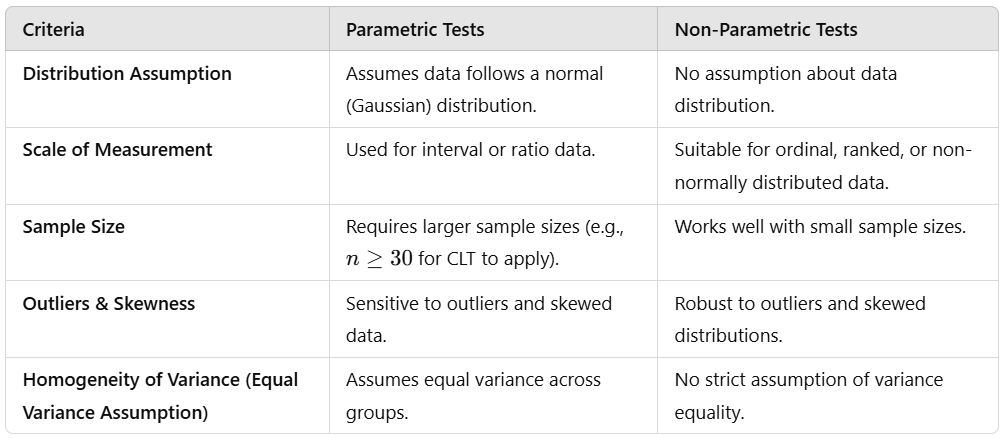
Data can also be classified as parametric or non-parametric, depending on the assumptions made about the data’s distribution. Parametric tests assume the data follows a specific distribution, usually a normal distribution, while non-parametric tests don’t rely on assumptions about the data’s distribution i.e., the data can be collected from a sample that does not follow a specific distribution.

Choosing Between Parametric and Non-Parametric Tests

The decision to use a parametric or non-parametric test depends on the characteristics of the dataset and the assumptions underlying statistical methods.

When to Use Parametric vs. Non-Parametric Tests?

How to Decide: Parametric or Non-Parametric?

Before choosing a test, check whether the normality assumption holds. You can assess this using:

1. Normality Tests (Decide if Parametric is Applicable)

2. Decision Rule:

• p > 0.05 → Data is normally distributed → Use parametric tests.
• p ≤ 0.05 → Data is NOT normally distributed → Consider non-parametric tests.

Common Parametric and Non-Parametric Tests

If Non-Parametric is Chosen, What Confirmatory Tests Can Be Performed?

Once non-parametric methods are chosen, you may perform robust confirmatory tests to validate findings.

1. Bootstrapping (Resampling Method)
   • Used to estimate confidence intervals without normality assumptions.
   • boot() function in R.
   • PROC SURVEYSELECT in SAS.
2. Permutation Tests
   • Compares observed data to randomly shuffled distributions.
   • coin package in R: independence_test()
   • PROC MULTTEST in SAS.
3. Robust Rank-Based Methods
   • Wilcoxon Signed-Rank Test (for paired samples).
   • Kruskal-Wallis with Dunn’s Post Hoc Test (for multiple comparisons).
4. Monte Carlo Simulations
   • Can validate findings using random sampling techniques.

Example: Choosing a Test Based on Data

Final Takeaway

1. First, check normality using tests like Shapiro-Wilk, K-S, or Q-Q plots.
2. If normality holds → Use parametric tests (t-test, ANOVA, Pearson, etc.).
3. If data is skewed, has outliers, or is ordinal → Use non-parametric tests (Mann-Whitney, Kruskal-Wallis, Spearman, etc.).
4. For confirmatory analysis in non-parametric cases, use bootstrapping, permutation tests, or Monte Carlo methods.