There is always uncertainty when estimating. This uncertainty is covered up with CI with a percent of confidence level say 95%. In critical industries such as healthcare, this may be 98%. If you are supposed to estimate at 95% confidence level that means 5% significance level. This is because the two values always add up to 100%, meaning the “remaining” 5% represents the significance level.
In terms of probability, this equates to 0.95 confidence level and 0.05 significance level which is your α (alpha). This significance level (α) represents the probability of rejecting a null hypothesis when it is true.
A 96% confidence interval implies that if we took 100 different samples and built a confidence interval from each sample, approximately 96 of those intervals would contain the true population parameter.
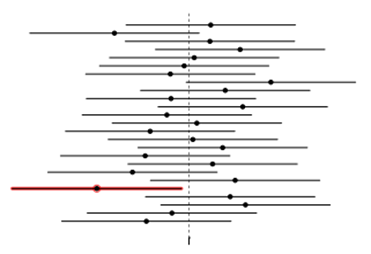
It does not mean there is a 96% probability the CI contains the true value. The figure above shows that if you take a sample of 25, then CI of 24 samples would contain the true average.
If area under curve is 1 & with 95% confidence level, we have alpha of 5 which is 2.5% on left tail and 2.5 on the right tail that we collectively call it as ‘critical region’. This critical region is the region for rejection of our hypothesis. If the observed test statistic from the sample falls in this critical region we reject null hypothesis.
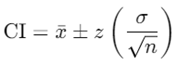
where x̄ is the sample mean, z is the critical value from the standard normal distribution, σ is the population standard deviation and n is the sample size. The CI has always a lower bound and upper bound value. These are the two values that define the range within which the true population parameter is likely to fall with a certain level of confidence.
In general, confidence intervals will always be of the form: point estimate ± CV × SE, where SE = SD(X)/√n & CV = Z*. For a 95% CI, CV = Z* = 1.96. Commonly used confidence levels in practice are 90%, 95%, 98%, and 99% and their respective Z scores are 1.645, 1.96, 2.326 and 2.576. Using the Z table, it is possible to find the appropriate Z* for any desired confidence level.
Let us work on a problem.
A company is testing the performance of a new drug to reduce blood pressure. A sample of 50 patients had their blood pressure reduced by an average of 8 mmHg, with a standard deviation of 3 mmHg. Assume the population follows a normal distribution. Construct a 95% confidence interval for the average reduction in blood pressure due to the drug.
Identify known quantities:
x̄ = 8 mmHg; n = 50; s = 3 mmHg; CL = 95%
Solve SE, Z, CI:
SE = s/sqrt(n) = 3/sqrt(50) = 0.4242641 Z = 1.96
> qnorm(1 – (1 – CL/ 2))
CI= x̄ ± Z⋅SE = (8 ± 1.96*0.4242641) = (7.16, 8.83)
We are 95% confident that the true mean reduction in blood pressure due to the drug lies between 7.16 mmHg and 8.83 mmHg.

