Probability quantifies uncertainty. It measures the likelihood of an event occurring, with values ranging between 0 (impossible) and 1 (certain). It has application in forecasting, risk analysis, medical trials, games, and decision-making.
Below are some of the terminologies that is good to know.
Experiment
An activity or process with uncertain outcomes (e.g., tossing a coin). The key characteristics of an experiment are:
- It has a defined procedure.
- It can be repeated under the same conditions.
- It generates outcomes that can be observed and recorded.
Trial
A trial is a single execution or instance of an experiment. Each trial produces one of the possible outcomes of the experiment. For example:
- In the experiment of rolling a die, each roll (where you get a specific number from 1 to 6) is a trial.
- In the experiment of flipping a coin, each flip (resulting in heads or tails) is a trial.
Rolling a die is an experiment while rolling the die once and getting a result of 4. So, while an experiment refers to the overall process that can produce multiple outcomes, a trial is one specific instance of that process.
Outcome
A possible result of an experiment (e.g., heads or tails).
Sample Space (S)
The set of all possible outcomes (e.g., for tossing a coin, S = {Heads, Tails}).
Event
A subset of outcomes from the sample space (e.g., getting heads).
Element
An individual outcome in the sample space. For example, 1, 2, 3, 4, 5, and 6 are elements of the sample space when rolling a die.
Subset
A set A is a subset of set B if all elements of A are also elements of B. In notation, this is written as A⊆B. For example, If A = {1,2} and B = {1,2,3,4} then A⊆B.
Types of Probability
1. Classical Probability
Assumes that all outcomes in the sample space are equally likely. It is often used in situations like games of chance like rolling a die or flipping a coin.
Formula:
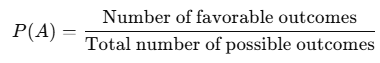
Example: Rolling a die
Total possible outcomes: {1,2,3,4,5,6}.
Probability of rolling a 4: P(4) = 1/6.
The probability of getting any specific number (e.g., 1 or 6) is the same for all six sides i.e., 1/6.
2. Empirical Probability
Based on observations or experimental data. Unlike classical probability, it doesn’t assume outcomes are equally likely.
Formula:
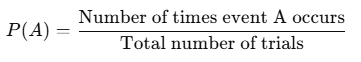
Example: Flipping a coin 50 times
Suppose the coin lands heads 30 times.
Probability of heads: P(Heads) = 30/50 = 0.6.
Conduct an experiment where you roll a die 20 times. If the number “4” appears 5 times, the empirical probability of rolling a 4 is: P(4) = 5/20 = 0.25.
3. Subjective Probability
Based on intuition, personal judgment, or expert opinion rather than actual data or equally likely outcomes. Commonly used in forecasting.
Examples: A weather forecaster predicts a 70% chance of rain tomorrow based on experience and current weather conditions.
A seasoned investor might estimate there’s a 60% chance of a stock price increasing tomorrow, based on market trends and personal analysis.

