Point estimate is a single value estimate of a population parameter. The sample mean (x̄) is a point estimate of the population mean (μ).
What Are Estimators in Point Estimation?
- An estimator is a rule, formula, or statistic that is used to estimate an unknown population parameter (e.g., population mean μ, variance σ2, or proportion p).
- In point estimation, the goal is to use sample data to compute a single value (point estimate) that serves as the best guess for the unknown parameter.
Examples of Estimators:
- Sample Mean (x̄): Used to estimate the population mean μ.
- Sample Proportion (p̂): Used to estimate the population proportion p.
- Sample Variance (s2): Used to estimate the population variance σ2.
Properties of Good Estimators
- Unbiasedness: An estimator is unbiased if its expected value is equal to the true value of the population parameter.
- Consistency: An estimator is consistent if it converges to the true value of the population parameter as the sample size increases.
- Efficiency: An estimator is efficient if it has the smallest variance among all unbiased estimators. The estimator with smallest MSE is always chosen.
- Sufficiency: An estimator is sufficient if it uses all the information in the data that relates to the parameter being estimated.
Why Do We Use Estimators?
Estimators are essential because:
- Populations Are Unobservable: We often cannot access data for the entire population, so we rely on a sample.
- Decision-Making: Estimators provide actionable insights to make predictions, draw conclusions, and make decisions.
- Inferential Analysis: They allow us to generalize findings from a sample to a population.
What Are Unbiased Estimators?
An unbiased estimator is one where the expected value of the estimator equals the true value of the parameter:
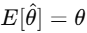
Examples:
- Sample Mean (x̄): Unbiased estimator of population mean μ.
- Sample Variance (s2): Unbiased estimator of population variance σ2 (if n−1 is used in the denominator instead of n).
Unbiasedness ensures that, on average, the estimator does not overestimate or underestimate the true parameter. An estimator is biased if:
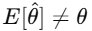
For example, using nnn instead of n−1 in the denominator of sample variance leads to a biased estimator.
What Are Approximations?
An approximation occurs when the exact calculation of a parameter is not feasible or when the estimator provides a close but not exact value of the parameter.
For example:
- The Central Limit Theorem (CLT) approximates the sampling distribution of the sample mean x̄ as a normal distribution for large sample sizes, even if the population is not normally distributed.
- Many estimation methods (e.g., Maximum Likelihood Estimation) rely on iterative numerical procedures that provide approximations to the true parameter.
Maximum Likelihood Estimator
The Maximum Likelihood Estimator (MLE) is a method of estimating a parameter by maximizing the likelihood function, which measures how likely the observed sample data is, given specific parameter values. Each distribution has its own likelihood function, and the MLE is derived accordingly.
Steps in MLE:
- Define the Likelihood Function: L(θ∣data)=P(data∣θ), where θ is the parameter to be estimated.
- Maximize the likelihood function L(θ)with respect to θ.
- The value of θ that maximizes L(θ) is the MLE.
Why Use MLE?
- It is widely used because it produces estimates with desirable properties, such as consistency (converging to the true value as sample size increases) and asymptotic efficiency (minimum variance for large samples).
Mean Square Error (MSE) and Estimators
The Mean Squared Error (MSE) of an estimator measures the average squared difference between the estimated value and the true parameter value. It is defined as:
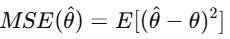
Purpose of MSE
MSE combines both:
- Variance of the estimator (how spread out the estimates are).
- Bias of the estimator (how far the estimator is from the true parameter value).
The estimator with the smallest MSE is generally preferred, as it minimizes the total error.
Let us understand this practically with a data (mtcars) in R.
1. Point Estimation for Mean
The sample mean x̄ can be used to estimate the population mean μ.
# Load mtcars dataset
> data(mtcars)
# Point estimate: Mean of mpg
> mean_mpg <- mean(mtcars$mpg)
> mean_mpg # 20.09062
This provides the sample mean, which serves as the point estimate for the population mean μ.
2. Maximum Likelihood Estimation (MLE)
The MLE for a parameter depends on the assumed distribution of the data. If we assume that mpg follows a normal distribution, we can estimate:
# MLE for normal distribution: Mean and Variance
> library(MASS)
> fit <- fitdistr(mtcars$mpg, “normal”) # Fit Normal Distribution
> fit

The MLE for the population mean μ is sample mean 20.09. This means that the most likely value for the average miles per gallon for cars is approximately 20.09. Likewise, the MLE for the population standard deviation σ is 5.93. It indicates the spread of the mpg values around the mean is approximately 5.93.
The values in parentheses are the standard errors for the MLE estimates. SE for Mean (1.0486446): This measures the uncertainty associated with the estimated mean (μ). SE for Standard Deviation (0.7415037): This measures the uncertainty associated with the estimated standard deviation (σ).
Smaller standard errors indicate greater confidence in the accuracy of the estimates. For example:
The true standard deviation likely lies close to 5.93 ± 0.74.
The true mean likely lies close to 20.09 ± 1.05.
What Do These Values Mean in Context?
i. Interpretation of the Mean:
The typical car in the dataset is estimated to have a fuel efficiency of 20.09 miles per gallon. If you were to randomly choose a car from the population, its expected mpg would be around this value.
ii. Interpretation of the Standard Deviation:
- The standard deviation tells us about the variability of
mpgvalues. From the empirical rule, in a normal distribution, about 68% of data falls within one standard deviation (SD) of the mean. Most of the cars in the dataset would have mpg values within 1 standard deviation of the mean:
μ±σ=20.09±5.93, or roughly between 14.16 and 26.02 mpg. - If the standard deviation were larger, the data would be more spread out, implying greater differences in fuel efficiency between cars.
iii. Confidence in Estimates:
- The small standard errors (relative to the estimates) suggest that the sample size (32 cars in
mtcars) is sufficient to provide reasonably accurate MLEs for the mean and standard deviation.
iv. Normality Assumption:
These results are based on the assumption that the mpg data follows a normal distribution. You should verify this assumption using visualizations like histograms or statistical tests (e.g., Shapiro-Wilk test).
3. Estimator Properties
Unbiased Estimator for Mean
The sample mean is an unbiased estimator of the population mean. You can verify this by simulating multiple samples from the data.
# Simulating unbiasedness
> set.seed(123)
> n <- 10 # Sample size
> samples <- replicate(1000, mean(sample(mtcars$mpg, n, replace = TRUE)))
> mean(samples) # Should be close to true mean
We see that the sample mean 20.08196 is close to true mean 20.090625.
Mean Squared Error (MSE)
To compute the MSE of an estimator, you can simulate data and compare the squared error with the true parameter.
# True mean of mpg
> true_mean <- mean(mtcars$mpg)
# Compute MSE for sample mean
> mse <- mean((samples – true_mean)^2)
> mse
4. Choosing the Best Estimator
# Comparing Mean and Median as estimators
> mean_error <- mean((samples – true_mean)^2) # MSE for mean
> median_samples <- replicate(1000, median(sample(mtcars$mpg, n, replace = TRUE)))
> median_error <- mean((median_samples – true_mean)^2) # MSE for median
> mean_error
> median_error
The estimator with the smaller MSE is preferred. When comparing the MSE of the mean (3.422775) and the median (5.129533), the estimator with the lower MSE is typically chosen as the better estimator. In this case, Since MSEmean<MSEmedian, we chose the MLE of the sample mean as the estimator for the true mean.

