The binomial distribution extends the concept of a Bernoulli trial, which involves a single experiment with only two possible outcomes. In a Bernoulli trial, the number of trials n is 1. The binomial distribution generalizes this to multiple independent trials, each with the same two possible outcomes. The binomial distribution models the number of successes in n independent trials, each with success probability p.
If X ~ Binomial(n,p), where: p – Probability of success (e.g., probability of a positive response) & n – Number of trials (e.g., number of people surveyed), .The PMF is given as
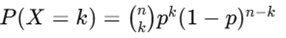
where x = 0,1,2,…,n.
The cdf is given as
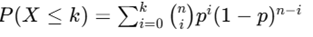
The mean is given as
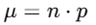
and the variance is given as
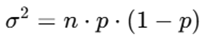
The binomial distribution can be applied in healthcare such as number of patients responding to a treatment out of a group and proportion of defective medical devices in a batch. Let us solve a problem to understand this better.
A drug has a 70% success rate in treating patients for a particular disease. For a trial with 10 patients, calculate:
1. Probability that exactly 7 respond positively (PDF).
P(X = 7) = (10C7)(0.7)7(0.3)3 = 0.2668
Note: 10C7 (n Choose x) means the number of ways to choose 7 items out of 10 items without regards to order. It is also known as the binomial coefficient.
10C4 = 10!/7!(10 – 7)! = 10!/(7!.3!) = (10⋅9⋅8⋅7!)/7!⋅3⋅2⋅1 = 720/6 = 120. In R, you can compute this as choose(10,7).
120⋅0.0823543⋅0.027 = 0.26682
There is a 26.68% chance that exactly 7 patients respond to the drug.
2. Probability that at most 6 respond positively (CDF).
P(X ≤ 6) = P(X = 0) + P(X = 1) + P(X = 2) +⋯+ P(X = 6)
P(X = 0) = (10C0)(0.7)0(0.3)10 = 1⋅1⋅0.0000059049=0.0000059049
P(X = 1) = (10C1)(0.7)1(0.3)9 = 10⋅0.7⋅0.000019683=0.000137781
P(X = 2) = (10C2)(0.7)2(0.3)8 = 45⋅0.49⋅0.00006561=0.0014467
P(X = 3) = (10C3)(0.7)3(0.3)7 = 120⋅0.343⋅0.0002187=0.009001692
P(X = 4) = (10C4)(0.7)4(0.3)6 = 210⋅0.2401⋅0.000729=0.03675691
P(X = 5) = (10C5)(0.7)5(0.3)4 = 252⋅0.16807⋅0.00243=0.1029193
P(X = 6) = (10C6)(0.7)6(0.3)3 = 210⋅0.117649⋅0.0081=0.2001209
P(X ≤ 6) = P(X = 0) + P(X = 1) + P(X = 2) +⋯+ P(X = 6) = 0.0000059049 + 0.000137781+ 0.0014467 + 0.009001692 + 0.03675691 + 0.1029193 + 0.2001209 = 0.3503892.
There is a 38.28% chance that at most 6 patients respond positively.
3. Probability that at least 5 respond positively (CDF).
P(X ≥ 5) = 1 − P(X < 5) = 1 − P(X ≤ 4)
Note: The expression 1 − P(X < 5) = 1 − P(X ≤ 4) is a key concept in probability and relates to how we compute complementary probabilities in discrete random variables.
P(X<5) means the probability that X, the random variable, takes on values less than 5. In a binomial distribution where X is a count (discrete), this includes values X = 0,1,2,3,4.
P(X ≤ 4) is the cumulative probability that X is less than or equal to 4. This is the sum of probabilities for X = 0,1,2,3,4.
P(X ≤ 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)
P(X = 0) = (10C0)(0.7)0(0.3)10 = 1⋅(1)⋅(0.3)10 = 0.00059
P(X = 1) = (10C1)(0.7)1(0.3)9 = 10⋅(0.7)⋅(0.3)9 = 0.00137
P(X = 2) = (10C2)(0.7)2(0.3)8 = 45⋅(0.7)2⋅(0.3)8 = 0.00900
P(X = 3) = (10C3)(0.7)3(0.3)7 = 120⋅(0.7)3⋅(0.3)7 = 0.03676
P(X = 4) = (10C4)(0.7)4(0.3)6 = 210⋅(0.7)4⋅(0.3)6 = 0.10292
P(X ≤ 4) = 0.00059 + 0.00137 + 0.00900 + 0.03676 + 0.10292 = 0.15064.
But P(X ≥ 5) = 1 − P(X < 5) = 1 − P(X ≤ 4) = 1 – 0.15064 = 0.84936.
The probability that at least 5 patients respond positively is: P(X ≥ 5) ≈ 0.849
You can simultaneously do these in R using the below syntax:
# Parameters
> n <- 10 # Number of patients
> p <- 0.7 # Success rate
# 1. Probability of exactly 7 successes (PDF)
> prob_exact_7 <- dbinom(7, size = n, prob = p)
> prob_exact_7
# 2. Probability of at most 6 successes (CDF)
> prob_at_most_6 <- pbinom(6, size = n, prob = p)
> prob_at_most_6
# 3. Probability of at least 4 successes (CDF)
> prob_at_least_4 <- pbinom(4, size = n, prob = p)
> prob_at_least_4

