The Negative Binomial Distribution is typically used to model the number of failures before achieving a fixed number of successes r, with success probability p.
If X ∼ Negative Binomial(r,p):
r – Number of successes we are waiting for.
p – Probability of success in a single trial.
Probability Mass Function (PMF):
The PMF of the Negative Binomial Distribution is:
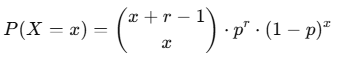
where x=0,1,2,… and (x+r−1)Cx is the binomial coefficient:
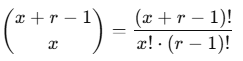
Mean:
r(1 – p)/r
Variance:
r(1 – p)/r2
Relationship Between Binomial and Negative Binomial
- Both involve Bernoulli trials, which are experiments with two possible outcomes: success or failure.
- In a binomial distribution, the focus is on the number of successes in a fixed number of trials (n) with a constant probability of success (p).
- In a negative binomial distribution, the focus is on the number of trials required to achieve a fixed number of successes (r) with a constant probability of success (p).
In binomial, we were interested in probability how many patients will respond positively. In negative binomial, in the same drug drial we are interested in finding the number of trials required to get r = 5 positive responses, with the probability of success per trial being p = 0.7.
When to Use Each?
- Use binomial distribution when the number of trials is fixed, and you’re counting the number of successes.
- Use negative binomial distribution when the number of successes is fixed, and you’re counting the number of trials.
Special Case Connection
The geometric distribution is a special case of the negative binomial distribution where r=1r = 1r=1. It models the number of trials until the first success.
Let us look at a problem. Suppose a new treatment is being tested, and the probability of success in a single trial is p = 0.7. You are interested in finding the probabilities of failures before observing r = 3 successes. Calculate:
1. Probability of exactly 4 failures (means P(X=4)) before achieving 3 successes (PMF).
For P(X=4):
Using the PMF formula, ((4+3-1)C4)⋅(0.7)3⋅(0.3)4 = 6C4⋅(0.7)3⋅(0.3)4 = 15⋅0.343⋅0.0081 = 0.0417315
The chance of having exactly 4 failures before achieving 3 successes is only about 4%.
2. Probability of at most 4 (meansP(X≤4)) failures (CDF).
P(X≤4)=P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)
P(X=0) = (2C0)⋅(0.7)3⋅(0.3)0 = 1⋅0.343⋅1 = 0.343
P(X=1) = (3C1)⋅(0.7)3⋅(0.3)1 = 3⋅0.343⋅0.3 = 0.3087
P(X=2) = (4C2)⋅(0.7)3⋅(0.3)2 = 6⋅0.343⋅0.09 = 0.18522
P(X=3) = (5C3)⋅(0.7)3⋅(0.3)3 = 10⋅0.343⋅0.027 = 0.092601
P(X=4) = 0.0417315 (calculated earlier)
P(X≤4) = 0.343 + 0.3087 + 0.18522 + 0.092601 + 0.0417315 = 0.971252
So, the chances of at more 4 failures before achieving 3 successes is about 97%.
3. Probability of at least 2 (means P(X≥2)) failures (CDF).
For P(X≥2) use the complement rule: P(X≥2) = 1 − P(X<2) = 1 − P(X≤1). From earlier:
P(X≤1) = P(X=0) + P(X=1) = 0.343 + 0.3087 = 0.6517
P(X≥2) = 1 − P(X≤1) = 1 – 0.6517 = 0.3483
So, the chances of at least 2 failures before 3 successes is 34.83%.
We can do this using R:
# Parameters
> r <- 3 # Number of successes
> p <- 0.7 # Probability of success
#1. Probability of exactly 4 failures
> prob_exact_4 <- dnbinom(4, size = r, prob = p)
> prob_exact_4
#2. Probability of at most 4 failures
> prob_at_most_4 <- pnbinom(4, size = r, prob = p)
> prob_at_most_4
#3. Probability of at least 2 failures
> prob_at_least_2 <- 1 – pnbinom(1, size = r, prob = p)
> prob_at_least_2

