Venn diagrams are visual representations of mathematical or logical sets. They show all possible logical relations between a finite collection of different sets.
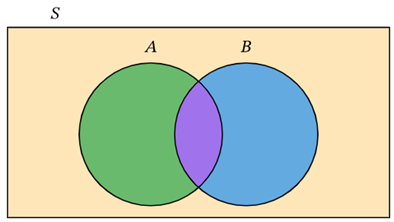
S: Sample space (universe).
A: Represented by green & purple region.
B: Represented by blue & purple region.
Union (A∪B): Represented as the area covered by both circles A and B with green, purple & blue region.
Intersection (A∩B): Represented as the area that has both A and B with purple region.
(A∪B) C: Represented by yellow region.
We will look into a problem to understand how the Venn diagram works.
Draw empty Venn diagram first.

The overlapping region represents intersection of events. We have 40 students who like both Math & Physics so the intersection is going to be 40. The number of students who like math is 70 but out of these 40 students like physics too. This gives the number of students who like math only is 70 – 40 = 30. Similarly, 60 – 40 = 20 students like physics only.
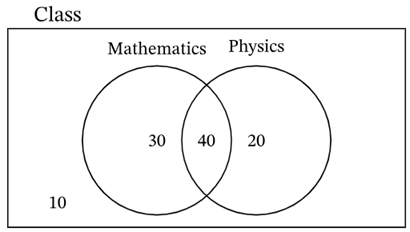
We put the 10 outside as the total should be 100 as that is the strength of the class. As a student is randomly selected and we know that only 30 students like math, we can divide this number with the total students i.e., 30/100 = 0.3. So, the probability that a randomly selected student who likes math only is 0.3 or you have a 30% chance to get a student randomly who likes math only.
