In statistics, the concepts of sample & population are fundamental to understanding how data is collected, analyzed, and interpreted. These concepts are central to the design of studies and experiments, the analysis of data, and the drawing of conclusions from that data. Whether you are conducting research in the fields of medicine, economics, social sciences, or any other discipline, a clear understanding of what constitutes a sample and a population is crucial.
Population is an entire group you want to study or draw conclusions about. It includes every member or item of interest.
For example, in medical research, the population might consist of all patients with a particular disease. In business, the population could be all customers who purchased a product in a given year. In education, the population might include all students in a school or district.
Sample is a smaller group selected from the population for the actual study. The sample should ideally represent the population well. The goal is to use the sample data to make inferences about the larger population.
For example, in medical research, a sample might be a group of 100 patients selected from the population of all patients with a disease. In business, a sample might be a survey of 500 customers out of the millions who purchased a product. In education, a sample might be a randomly selected group of students from a school. Using a sample is often more practical and cost-effective than studying the entire population, especially when the population is large and spread out. Samples can be drawn using various sampling methods, such as random sampling, stratified sampling, or cluster sampling, depending on the study’s objectives and the nature of the population.
The field of inferential statistics enables you to make educated guesses about the numerical characteristics of large groups. The logic of sampling gives you a way to test conclusions about such groups using only a small portion of its members.
Parameter & Statistic:
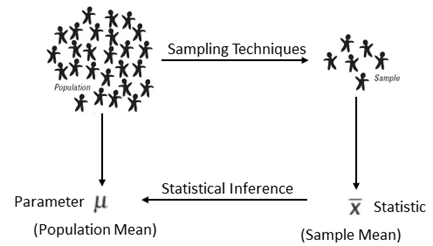
A parameter describes a characteristic of an entire population, while a statistic describes a characteristic of a sample. Inferential statistics allows you to make an informed estimate about a population parameter by using a statistic calculated from a randomly selected sample from that population. The figure below shows relationship between samples & population.
Sampling Methods
Simple Random Sampling: Every individual in the population has an equal chance of being selected. This method minimizes bias but requires a complete list of the population.
Stratified Sampling: The population is divided into subgroups (strata) that share similar characteristics, and a sample is drawn from each stratum. This ensures that the sample is representative of all strata.
Cluster Sampling: The population is divided into clusters, usually based on geographical areas or natural groupings. A sample of clusters is selected, and all members of the chosen clusters are included in the sample.
Importance of Sample Size:
The size of the sample is a critical factor in determining how accurately the sample represents the population. Larger samples generally provide more reliable estimates of the population parameters because they reduce the impact of random variations and outliers. However, very large samples can be costly and time-consuming, so researchers must balance the need for accuracy with the constraints of time and resources.
Sampling Error and Bias:
Sampling error refers to the difference between a sample statistic and the corresponding population parameter. This error occurs because the sample is only a subset of the population, and it may not perfectly represent the population.
Bias occurs when certain members of the population are more likely to be included in the sample than others, leading to a sample that is not representative of the population. Bias can occur due to poor sampling methods, such as non-random sampling or under-coverage, where certain groups are not adequately represented in the sample.
Role of Statistical Inference:
Statistical inference is the process of using data from a sample to make estimates or test hypotheses about the population. The goal is to make generalizations about the population based on the sample data, with an understanding of the uncertainty involved.
Two key concepts in statistical inference:
Confidence intervals (CI): These provide a range of values within which the population parameter is likely to lie, with a certain level of confidence (e.g., 95% confidence interval).
Hypothesis testing: This involves testing a hypothesis about a population parameter using sample data, often to determine if there is enough evidence to reject a null hypothesis.
The concepts of sample and population are applied across various fields:
Medicine: In clinical trials, a sample of patients is used to test the efficacy of a new drug. The results are then generalized to the entire population of patients with the disease.
Market Research: Companies often survey a sample of consumers to understand preferences, which helps in making decisions about product development and marketing strategies.
Political Polling: Pollsters survey a sample of voters to predict the outcome of elections, assuming that the sample represents the voting population.
Environmental Studies: Scientists might sample water from different parts of a lake to assess the overall health of the aquatic ecosystem.
Why is a Sample Size of > 30 Considered Sufficient?
The guideline that a sample size greater than 30 is sufficient comes from statistical principle the Central Limit Theorem (CLT). According to the CLT, the sampling distribution of the sample mean will approach a normal distribution, regardless of the population’s original distribution, as the sample size increases. This property allows statisticians to make inferences about a population from a sample.
Reasons for the Sample Size Guideline:
Normality Assumption: For many statistical tests and methods (like t-tests & CI), there is an assumption that the data is normally distributed. A sample size ≥ 30 is often enough for the sample mean to approximate a normal distribution, even if the underlying population distribution is not normal.
Minimizing Error: A larger sample size reduces the standard error of the mean, which increases the precision of the estimated population parameters. For most practical purposes, a sample size greater than 30 is sufficient to ensure that the sampling distribution is approximately normal, which helps in reducing errors in hypothesis testing and confidence intervals.
Practicality and Cost: While larger samples provide more precise estimates, collecting data is often expensive and time-consuming. A sample size of 30 strikes a balance between statistical accuracy and practical feasibility, particularly in fields like social sciences, where resources may be limited.
