In statistics, error and residual are two important concepts used to measure the deviation between observed and predicted values in data analysis. While they are often confused, they have distinct definitions and purposes.
Error
Error refers to the difference between the true value of a population parameter and the observed (sample) value. It’s the discrepancy between the actual population value and the value predicted by a model. Since we often do not know the true value, errors are theoretical.
Error=yi−μ
where yi is the observed value and μ is the true population value. Since the population mean is unknown in most practical applications, we cannot compute the exact error.
Residual
Residuals are the difference between observed values and the predicted values generated by a model. It’s an observable measure based on the sample data and the fitted model.
Residual = yi−ŷ
where yi is the observed value, and ŷ is the predicted value from the model. Residuals are measurable and reflect how well a model fits the data. In regression analysis, they are used to diagnose the goodness of fit of the model.
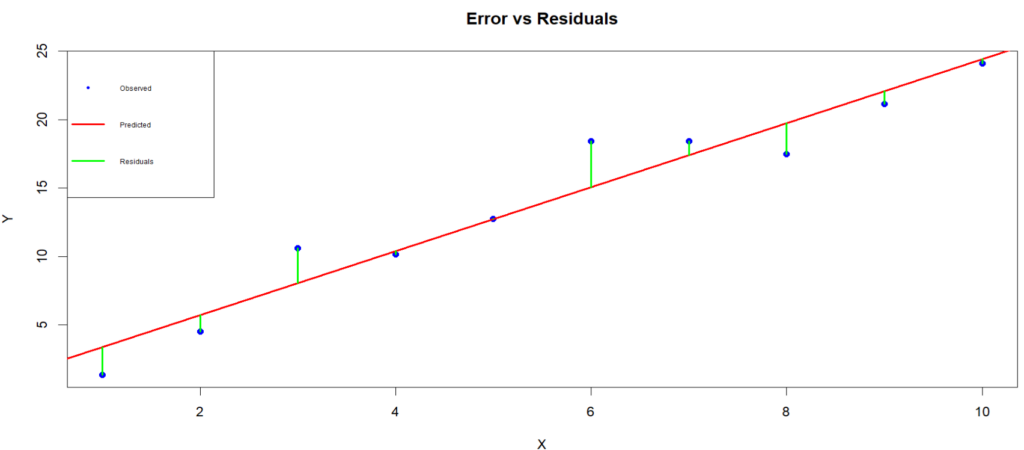
Residuals (green lines) are measurable deviations from the predicted values (ŷ), calculated using the sample data. To illustrate errors alongside residuals in the same plot, we need to make an assumption about the true population line (μ), which we rarely know in practice. For the sake of visualization, assume a hypothetical true population regression line and plot the errors as the difference between the observed points and this true line.
