The central tendency is the extent to which all the data values group around a typical or
central value.
1. Mean (Arithmetic Mean)
The sample mean is denoted x̄ (read “x-bar”) and is simply the arithmetic average of the observations.
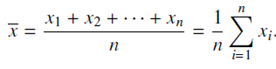
Mean is sensitive to extreme values. They can be used if the data is not highly skewed without extreme observations.
> mean(mtcars$mpg
2. Trimmed Mean
A trimmed mean is a statistical measure that calculates the average of a dataset by removing a certain percentage of the highest and lowest values. This process is also known as truncating the mean or truncated average.
The trimmed mean helps to reduce the impact of outliers and provides a more accurate representation of the central tendency of the data. For example, the 50% trimmed mean is the mean of the values between the upper and lower quartiles, and the 90% trimmed mean is the mean of the values after truncating the lowest and highest 5% of the values.
> mean(mtcars$mpg, trim = 0.05)
3. Harmonic Mean
The Harmonic Mean (HM) is the reciprocal of the arithmetic mean of reciprocals. It is particularly useful when averaging rates or ratios, like speed or density. It is very sensitive to small values & gets reduced significantly. There is no syntax for HM. We have to create a function to get the values.

x <- mtcars$mpg
harmonic_mean <- function(x) {
length(x) / sum(1 / x)
}
harmonic_mean(x)
4. Geometric Mean (GM)
The Geometric Mean (GM) is the n-th root of the product of n numbers. It is used to find the average in multiplicative processes. It is always less than or equal to the arithmetic mean.
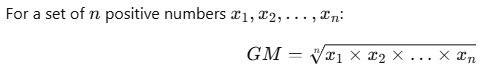
> x <- mtcars$mpg
> geometric_mean <- function(x) {
prod(x)^(1 / length(x))
}
> geometric_mean(x)
5. Median
The sample median x͂ is robust to extreme values. To calculate sample median, the observations are to be sorted in increasing order then x͂ is the value of the middle observation which lies in position (n+1)/2, otherwise, the average of the middle 2 observations are taken as the value.
> median(mtcars$mpg)
