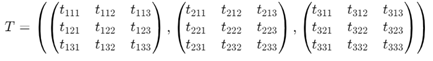A scalar is a single number used to measure magnitude. It is the simplest type of data in mathematics and data science. For example, temperature: 30°C & speed: 60 km/h.
> x = 5
Vectors: A vector is an ordered list of numbers. Vectors are used to represent data points in multi-dimensional space. For example, marks obtained out of 100 in a class of 5 students.
> y = c(67, 78, 89, 90, 92)
A matrix is a rectangular array of numbers, symbols, or expressions arranged in rows and columns. The individual items in a matrix are called its elements or entries. Matrices are used to represent and solve systems of linear equations, perform transformations, and manage data.
> A = matrix(c(1, 2, 3, 4, 5, 6, 7, 8, 9), nrow = 3, ncol = 3, byrow = TRUE)
A tensor is a multi-dimensional generalization of scalars, vectors, and matrices. Tensors are used extensively in data science, especially in machine learning and deep learning.
Scalar: A single number (0-dimensional tensor or first order tensors).
Vector: A 1-dimensional array of numbers (1-dimensional tensor).
Matrix: A 2-dimensional array of numbers (2-dimensional tensor).
A 3rd-order tensor could be represented as Tijk, where i, j and k are indices that run over the dimensions of the tensor.
For example, in a 3D Cartesian coordinate system, a 3rd-order tensor might look like: