Bernoulli Trial

A Bernoulli trial is a fundamental concept in probability theory and statistics. It refers to a random experiment where there are only two possible outcomes: “success” and “failure.” Bernoulli trials form the basis for many important probability distributions and concepts, including the Binomial distribution and the concept of independent events.

Key Characteristics of Bernoulli Trials

1. Two Outcomes: Each trial results in exactly one of two outcomes, typically labeled as “success” (often denoted by 1) and “failure” (often denoted by 0).
2. Probability of Success: The probability of success is denoted by p, where 0≤p≤1.
3. Probability of Failure: The probability of failure is denoted by qq, where q = 1 – p.
4. Independence: Each trial is independent of the others, meaning the outcome of one trial does not affect the outcome of another.

Mathematical Representation

If X represents the outcome of a Bernoulli trial, then X is a Bernoulli random variable with the following properties:

Probability Mass Function (PMF):

A discrete random variable X is said to be a Bernoulli random variable with parameter p, shown as X ∼ Bernoulli(p), if its PMF is given by

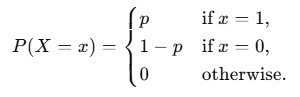
Expected Value (Mean):

E[X] = p

Variance:

Var(X) = p(1−p)

Example: The Bernoulli distribution models a single trial with two possible outcomes: success (X = 1) or failure (X = 0).The parameter p (where 0 ≤ p ≤ 1) fully defines the distribution.

Suppose X represents whether a coin flip results in heads (X = 1) or tails (X = 0), and the coin has a probability p = 0.6 of landing heads. The PDF is:

P(X = 0) = 1 – 0.6 = 0.4.

Real-Life Examples of Bernoulli Trials

1. Coin Toss: Flipping a fair coin is a classic example of a Bernoulli trial, where the outcomes are “heads” (success) and “tails” (failure). The probability of getting heads is p=0.5 and the probability of getting tails is q=0.5.
2. Quality Control: In a manufacturing process, inspecting a product for defects can be modeled as a Bernoulli trial. The outcomes are “defective” (success) or “non-defective” (failure), with pprepresenting the probability of a defect.
3. Medical Testing: In a medical test for a disease, each test can be considered a Bernoulli trial with outcomes “positive” (success) and “negative” (failure). The probability p represents the likelihood of a positive test result.

Applications in Probability Distributions

• Binomial Distribution: A Binomial distribution arises from the sum of multiple independent Bernoulli trials. For example, if we flip a coin 10 times, the number of heads follows a Binomial distribution with parameters n=10n = 10 and p=0.5p = 0.5.
• Geometric Distribution: The number of trials needed to get the first success in a sequence of Bernoulli trials follows a Geometric distribution. For instance, the number of attempts needed to get the first heads when repeatedly flipping a coin.
• Negative Binomial Distribution: The number of trials needed to achieve a specified number of successes follows a Negative Binomial distribution.