A percentile is a measure of position, not dispersion. Percentiles represent the position of a data point inside a data set by splitting it into hundredths. For example, 10th percentile would mean 10% ≤ n(0.10) or equivalently 90% ≥ n(0.10). This means that percentiles can help you determine the position of a specific data point within a data set. For example, a percentile can divide a data set into hundredths, such as the 1st percentile, 2nd percentile, and so on.
Let us discuss with a problem. To determine a percentile rank, we prepare a frequency distribution table e.g., of the length of stay for patients discharged from DRG 127, Heart Failure and Shock. The length of stay ranges from 1 day to 27 days and are ranked from the longest to the shortest length of stay. The frequency ‘f’ is given here. We want to know the percentile rank for a length of stay of five days. The length of stay data is given below.
3,3,2,8,7,4,3,3,10,10,3,9,6,5,2,2,2,3,5,4,5,11,10,2,8,7,4,1,2,11,6,2,2,3,5,7,7,5,8,1,2,3,7,4,17,11,3,1,2,14,5,2,3,27,5,5,6,2,7,8.
> los<-c(3,3,2,8,7,4,3,3,10,10,3,9,6,5,2,2,2,3,5,4,5,11,10,2,8,7,4,1,2,11,6,2,2,3,5,7,7,5,8,1,2,3,7,4,17,11,3,1,2,14,5,2,3,27,5,5,6,2,7,8)
> sort(los, decreasing = TRUE)
> los_table <- as.data.frame(table(los)) # Create frequency table
> los_table$cumf <- cumsum(los_table$Freq) # Calculate cummulative frequency
> los_table$ptile <- los_table$cumf / sum(los_table$Freq) * 100 # Calculate percentile rank
> print(los_table)
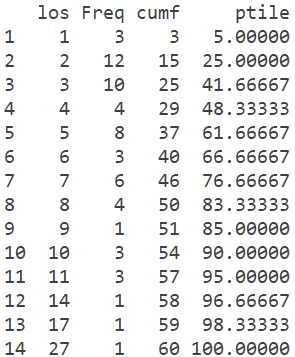
So, the percentile rank for a length of 5 days = 37/60*100 = 61.7%.
The interpretation is that 61.7% of the discharges from DRG 127 have a length of stay of five or fewer days.
